Zuerst gehen wir kurz auf den Begriff der dynamischen Programmierung ein, bevor wir zum sogenannten Rucksackproblem, einem Optimierungsproblem, kommen.
WAS IST DYNAMISCHE PROGRAMMIERUNG?
Die dynamische Programmierung dient zur Lösung eines Optimierungsproblems durch algorithmische Verfahren. Das Problem wird in Teilprobleme zergliedert und es werden systematisch Zwischenergebnisse gespeichert.
Mit dem Namen1 bezeichnet man also ein Algorithmen-Entwurfsparadigma2. Es ist Ihnen möglicherweise noch aus dem Mathematikunterricht bekannt.
Obwohl es da üblicherweise nicht erwähnt wird, ist nämlich das zeilenweise Ausfüllen des pascalschen Dreiecks3 (also die Ermittlung bestimmter Binomialkoeffizienten) tatsächlich dynamische Programmierung! Durch die übliche Berechnungsreihenfolge sind günstigerweise immer alle Werte, die man zum Ausfüllen der nächsten Zeile braucht, schon in der darüber liegenden Zeile vorhanden.
Allgemeiner besitzen manche algorithmischen Probleme eine rekursive Formulierung, bei der aus den Lösungen für kleinere Instanzen die Lösungen für größere Instanzen zusammengesetzt werden können. Wie die Teilprobleme gestaltet sind und wie sie sich zusammensetzen lassen, hängt dabei sowohl vom Problem selbst als auch von der Wahl der Formulierung ab.
DYNAMISCHE PROGRAMMIERUNG MIT ÜBERLAPPENDEN TEILINSTANZEN
Wir sprechen weiter besonders bei Optimierungsproblemen davon, dass diese Probleme eine „optimale Teilstruktur“ haben. Es kann dabei jedoch vorkommen, dass man überlappende Teilinstanzen erhält, da beim rekursiven Auswerten die gleichen Teilinstanzen mehrfach auftreten. Es fällt sofort auf, dass es überflüssig (und somit unerwünscht) ist, diese mehrfach zu lösen.
Abhilfe schafft zunächst ein zusätzlicher Zwischenspeicher4, in dem die Lösungen von Teilinstanzen gespeichert werden, um ihre erneute Lösung zu vermeiden. Vor einem rekursiven Aufruf wird dann geprüft, ob für die auszuwertenden Argumente bereits ein Ergebnis vorliegt.
Die Struktur des Zwischenspeichers – typischerweise eine Tabelle – kann dabei direkt aus der Signatur der in der rekursiven Formulierung verwendeten Funktion ermittelt werden. Dieser Ansatz wird als "Memoisation" bezeichnet. Er vermeidet die mehrfache Lösung gleicher Teilinstanzen, behält aber die rekursive Auswertung bei.
Durch eine mehr oder weniger geschickte Wahl der Berechnungsreihenfolge können wir aber auf die rekursive Auswertung ganz verzichten, indem diese Tabelle iterativ5 ausgefüllt wird. Dabei beginnen wir bei den kleinsten Teilinstanzen, deren Lösungen wir direkt ablesen können.
Im Folgenden stellen wir nun zwei auf dynamischer Programmierung basierende Ansätze für das Rucksackproblem vor.
1. ABZÄHLEN DES GEWICHTS
Beim ersten Ansatz6 werden in einem Zustandsraum P auf der ersten Achse die Indices eines Anfangsstücks der n Items aufgetragen und auf der zweiten Achse das Gewicht. Als obere Schranke für das maximale Gewicht einer optimalen Lösung verwenden wir die Kapazität C des Rucksacks.


2. ABZÄHLEN DES PROFITS
Beim zweiten Ansatz8 werden in einem Zustandsraum W auf der ersten Achse die Indices eines Anfangsstücks der n Items aufgetragen und auf der zweiten Achse der Profit. Als obere Schranke P für den maximalen Profit können wir die Summe aller vorkommenden Profite verwenden9.
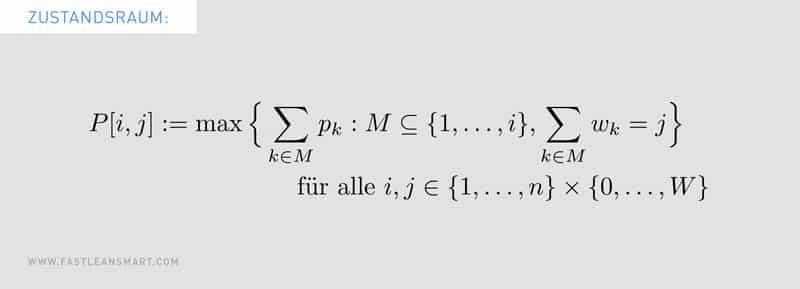

ERMITTLUNG EINER OPTIMALEN AUSWAHL
Die beiden oben beschriebenen Algorithmen liefern zunächst nur den optimalen Zielfunktionswert, aber keine optimale Auswahl der Items. Deshalb haben wir zusätzlich Backtracking implementiert.
Dabei wird mit einem optimalen Zustand begonnen. Durch Vergleiche wird ermittelt, aus welchem Zustand er durch die jeweilige Rekurrenzgleichung entstanden sein kann. Dementsprechend wird das zur jeweiligen Zeile des Zustandsraums gehörende Item entweder mit in die Auswahl aufgenommen (oder nicht) und es wird zum Vorgängerzustand übergegangen. Dieser Schritt wird so lange iteriert, bis wir in der ersten Zeile des Zustandsraums angekommen sind.
Das Backtracking ist für beide Algorithmen relativ leicht zu implementieren und hat jeweils eine lineare Laufzeitschranke.
IMPLEMENTIERUNG
Wir haben beide Algorithmen in C# implementiert10, wobei die Indizierung der Items natürlich bei 0 und nicht bei 1 beginnt. In der jeweils auszuwertenden Zeile des Zustandsraums können die Einträge unabhängig voneinander (und somit durch verschiedene Threads) ermittelt werden. Da es vergleichsweise einfach war, haben wir also beide Algorithmen parallelisiert.
Zusätzlich haben wir einen Preprocessing-Schritt11 vorangestellt, der vor der eigentlichen Lösung der Instanz diejenigen Items entfernt, auf die in einer optimalen Lösung verzichtet werden kann. Genauer sind dies Items mit Profit 0 oder kapazitätsüberschreitendem Gewicht und Items mit geringem Profit innerhalb einer Gewichtsklasse.
Schließlich haben wir mithilfe von Linq12 den oben erwähnten Backtracking-Schritt implementiert.
Wir haben die Implementierung auf einer Instanzbibliothek13 mit bekannten Optima getestet14. Wer möchte, kann das gerne selbst ausprobieren. Dazu müssen die als „Small Coefficients“ klassifizierten Instanzen15 ins Verzeichnis gleichen Namens kopiert werden.
Die Auswertungen sind als Komponententests implementiert und können z.B. in Visual Studio über MSTest gestartet werden. Es ist dabei allerdings zu beachten, dass die Implementierungen sehr speicherintensiv sind, da der Zustandsraum explizit dargestellt wird.
FAZIT
Der erste Ansatz, bei dem das Gewicht abgezählt wird, ist etwas unmittelbarer, da das maximale Gewicht einer optimalen Lösung direkt aus der Instanz abgelesen werden kann und die Werte der Zustände direkt den Zielfunktionswerten von zulässigen Lösungen entsprechen. Beim zweiten Ansatz hingegen muss eine Schranke für den optimalen Profit erst künstlich erzeugt werden, was durch Relaxierung oder einen Approximationsalgorithmus möglich ist.
Allerdings wachsen sowohl die Laufzeit als auch der Speicherbedarf beider Algorithmen exponentiell an. Die Laufzeitschranken sind zwar polynomiell in der Anzahl der Items beschränkt, aber es gehen Zahlenwerte der Items16 in die Laufzeitschranken ein, sodass diese dennoch exponentiell in der Länge ihrer Eingaben wachsen können.
Die implementierten Algorithmen können in diesem Sinne nicht als effizient angesehen werden17, was bei einem NP-schweren Optimierungsproblem18 aber auch nicht zu erwarten war.
Effiziente Algorithmen (wie etwa der PowerOpt , der grundsätzlich ebenfalls für Packungsprobleme des hier vorgestellten Typs geeignet ist) haben ein wesentlich günstigeres Skalierungsverhalten. Sie erfüllen ggf. sogar Echtzeit-Anforderungen.
Schließlich sei noch der Vollständigkeit halber darauf hingewiesen, dass der zweite Algorithmus als Grundlage eines Approximationsschemas19 verwendet werden kann, was bei dem ersten Algorithmus jedoch nicht möglich ist.
Weitere Artikel:
➡ TOPOLOGISCHE SORTIERUNG
➡ DAS RUCKSACKPROBLEM
➡ TRAVELING SALESPERSON PROBLEM
➡ GANTT CHARTS IN DER TOURENPLANUNG
Thomas H. Cormen et al.: Introduction to Algorithms (Third Edition), MIT Press, 2009, S. 359ff.
Da der Ansatz mehrfach entdeckt wurde, wird die Tabelle auch Tartaglia-Dreieck (nach Niccolò Tartaglia), Yang-Hui-Dreieck (nach 楊輝), oder Chayyām-Dreieck (nach عمر خیام) genannt.
Die Datenstruktur, in der die Lösungen gespeichert werden, wird im Kontext der dynamischen Programmierung auch als Zustandsraum und die Einträge als Zustände bezeichnet.
Das ist besonders dann interessant, wenn in der verwendeten Programmiersprache Rekursion nicht direkt unterstützt wird oder die Verwendung eines expliziten Stacks nicht möglich ist.
Robert Sedgewick: Algorithmen, Addison-Wesley, 1991, 674–677; Jon Kleinberg & Éva Tardos: Algorithm Design, Addison-Wesley, Pearson, 2005, Kapitel 6 (in dem das Rucksackproblem aus dem Teilsummenproblem entwickelt wird) und S. 271ff.
In den Implementierungen wird keine explizite Darstellung der „Werte mit unendlichem Betrag“ verwendet, was dann Fallunterscheidungen während der Berechnung oder die Verwendung eines angepassten Typs nötig gemacht hätte. Stattdessen kommen instanzabhängige Schranken zum Einsatz.
Klaus Jansen & Marian Margraf: Approximative Algorithmen und Nichtapproximierbarkeit, de Gruyter, 2008.
In unserer Implementierung verwenden wir allerdings eine durch Relaxierung gewonnene, tendenziell kleinere obere Schranke.
Die Implementierung (nicht unmittelbar lauffähig ohne die erwähnte Instanzenbibiothek) ist als Projektmappe für Visual Studio verfügbar unter https://github.com/DbRRaU6m/Knapsack
Eugene Lawler: Fast Approximation Algorithms for Knapsack Problems, Mathematics of Operations Research 4(4), 1979.
Joseph Albahari: Linq – kurz & gut, O‘Reilly, 2016.
http://hjemmesider.diku.dk/~pisinger/codes.html
Die Tests wurden als Komponententests mit MSTest realisiert.
http://www.diku.dk/~pisinger/smallcoeff_pisinger.tgz
Solche Laufzeitschranken werden als pseudopolynomiell bezeichnet.
Robert Sedgewick: Algorithmen, Addison-Wesley, 674–677, 1991.
Hans Werner Lang: Algorithmen in Java, Oldenbourg Wissenschaftsverlag, Kap. 11, 2006.
Oscar H. Ibarra & Chul E. Kim: Fast Approximation Algorithms for the Knapsack and Sum Of Subset Problems, Journal of the ACM 22(4):463–468, 1975.