20. Oktober 2017 · Dr. Florian Diedrich
I. DEFINITION & MOTIVATION
Die Eingabe unseres Algorithmus besteht aus einem Graphen2 mit n Knoten. Die Kanten sind gerichtet; dies bedeutet, dass eine Kante immer von einem Knoten u zu einem Knoten v verläuft. Ist dies der Fall, wird u als Vorgänger von v und v als Nachfolger von u bezeichnet. Um die verschiedenen Rollen der beteiligten Knoten anzudeuten, werden in visuellen Darstellungen Pfeile verwendet. Fig. 1 zeigt ein Beispiel eines solchen Graphen.
Eine topologische Sortierung ist eine Reihenfolge der Knoten, bei der für jeden Knoten u alle seine Nachfolger v später vorkommen als u – wir möchten also die Knoten in eine Reihenfolge bringen, in der die Kanten immer nur „nach rechts“ zeigen. Fig. 3 zeigt eine solche Reihenfolge. Dabei fällt auf, dass eine topologische Sortierung in der Regel nicht eindeutig ist; beispielsweise können L, M und K beliebig vertauscht werden.
Das Problem der Bestimmung einer topologischen Sortierung wollen wir zunächst aus der Ablaufplanung motivieren. Wir stellen uns dazu vor, dass die Knoten des Graphen zu erledigende Aufgaben sind. Die Kanten stellen dabei Reihenfolgebedingungen dar. Verläuft eine Kante von A nach B, so muss A vor B erledigt werden – beispielsweise muss bei A ein Werkzeug abgeholt werden, dass zur Durchführung von B nötig ist.
Zur Motivation aus der Software-Entwicklung stellen wir uns vor, dass programmatisch ein SQL-Statement erzeugt werden soll. Genauer sollen die Fremdschlüsselbeziehungen einer Menge von Datenbanktabellen in Join-Statements verwendet werden. Dazu ist es nötig, die Tabellen in eine Reihenfolge zu bringen, bei der in den Join-Bedingungen weiter rechts im Statement stehender Join-Faktoren nur Tabellen vorkommen, die bereits weiter links im Statement aufgetreten sind.
II. EIN ALGORITHMUS FÜR TOPOLOGISCHE SORTIERUNG
Der Begriff der topologischen Sortierung ist seit spätestens 19303 in der Fachliteratur nachweisbar und wird typischerweise in Algorithmik-Lehrbüchern4 behandelt; die Erzeugung einer topologischen Sortierung war ferner Algorithmus der Woche5 im Informatik-Jahr 2006.
Üblicherweise wird zum Erzeugen einer topologischen Sortierung ein Algorithmus vorgestellt, der auf iterativer Suche von Knoten mit Eingangsgrad 0 basiert, wobei der Eingangsgrad etwa in einem unterstützenden Array verwaltet wird. Ein Knoten ohne Vorgänger wird dann als nächster Kandidat in die topologische Sortierung übernommen und der Eingangsgrad aller seiner Nachfolger dekrementiert. Dieser Algorithmus kann stackfrei6 implementiert werden, was ihn für den Einsatz in sehr eingeschränkten technischen Umgebungen attraktiv macht.
Interessanterweise kann aber eine topologische Sortierung auch durch modifizierte Tiefensuche7 erzeugt werden. Fig. 2 zeigt einen DFS-Wald (mit etwas suggestivem Layout) für den Graphen8 aus Fig. 1, wobei die Zahlen in den Knoten die Besuchsreihenfolge angeben. Bäume stellen wir so dar, dass die Wurzel oben ist – dies ist passend, denn „in der Informatik wachsen die Bäume nicht in den Himmel“9. In Fig. 2 geben die Zahlen an den Knoten jeweils die Reihenfolge an, in der mit dem Besuch des Knotens begonnen wird. Die gezeigten Kanten sind Baumkanten, während Vorwärts-, Rückwärts- und Querkanten nicht gezeigt werden. Da der Graph aus Fig. 1 nicht stark zusammenhängend ist, muss die Tiefensuche insgesamt zweimal begonnen werden, in unserem Beispiel in A und J.

Fig. 1: gerichteter Graph

Fig. 2: DFS-Wald für den gerichteten Graphen aus Fig. 1
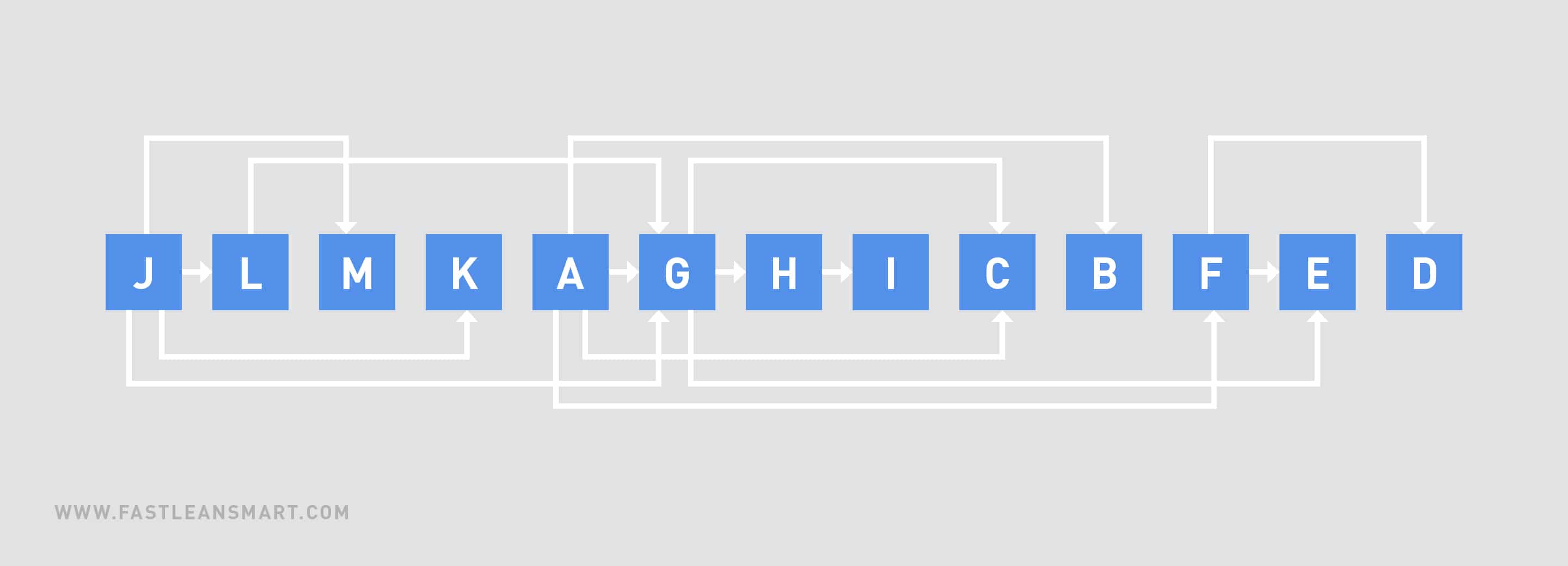
Fig. 3: Topologische Sortierung für den gerichteten Graphen aus Fig. 1
Unsere Implementierung benutzt einen generischen Typen T für die Knoten und besteht im Wesentlichen aus zwei Funktionen. Die Signatur der ersten Funktion erschließt sich möglicherweise nicht unmittelbar.
Implementierung:
public static IEnumerable<T> Sort<T>(IEnumerable<T> Nodes,
Func<T, IEnumerable<T>> Successors,
out bool HasCycle)
{
var VisitedNodes = new HashSet<T>();
var Result = new List<T>();
HasCycle = false;
foreach (var iNode in Nodes.Where(iNode => false == VisitedNodes.Contains(iNode)))
{
Visit(iNode, Successors, VisitedNodes, Result, ref HasCycle);
if (HasCycle)
{
break;
}
}
return HasCycle ? null : Result;
}
Wir stellen keine Typanforderungen (wie etwa Implementierung eines Knoten-Interfaces) an T, sondern verwenden stattdessen ein weiteres Argument Successors, das für jeden Knoten seine Nachfolger zurückgibt. So erhalten wir eine möglichst lose Kopplung zwischen unserer Implementierung und der Umgebung, in der sie aufgerufen wird. Das Ausgabe-Argument HasCycle soll explizit angeben, ob der eingegebene Graph einen Kreis besitzt (und somit die Erzeugung einer topologischen Sortierung unmöglich ist). Die Rückgabe ist eine topologische Sortierung der Knoten (falls der eingegebene Graph kreisfrei ist) und null andernfalls.
Im eigentlichen Rumpf iterieren wir über die unbesuchten Knoten des eingegebenen Graphen, für die wir die unten stehende Besuchsfunktion aufrufen, die die eigentliche Tiefensuche ausführt. Auf diese Weise stellen wir u. A. sicher, dass die Tiefensuche auf allen schwachen Zusammenhangskomponenten der Eingabe ausgeführt wird.
Ein Preis der von uns angestrebten losen Kopplung ist die Unmöglichkeit, die bereits besuchten Knoten direkt zu markieren. Stattdessen verwenden wir VisitedNodes als Hilfsdatenstruktur, um sie zu speichern. Diese Hilfsdatenstruktur und eine Liste für die Ausgabe werden zusätzlich an Visit übergeben, wodurch wir eine recht ähnliche Signatur wie bei Sort erhalten.
Implementierung:
private static void Visit<T>(T iNode,
Func<T, IEnumerable<T>> Successors,
HashSet<T> VisitedNodes,
List<T> iList,
ref bool HasCycle)
{
if (false == VisitedNodes.Contains(iNode))
{
VisitedNodes.Add(iNode);
foreach (var jNode in Successors(iNode))
{
Visit(jNode, Successors, VisitedNodes, iList, ref HasCycle);
}
iList.Insert(0, iNode);
}
HasCycle |= false == iList.Contains(iNode);
}
Die eigentliche Erzeugung der topologischen Sortierung erfolgt dabei insgesamt nach dem Ansatz, einen besuchten Knoten erst dann an den Anfang der Ausgabe zu stellen, wenn alle seine Nachfolger besucht sind. Wir erhalten dadurch die gewünschte „Ausrichtung“ der Kanten.
III. FAZIT
In diesem Blog-Artikel haben wir das Problem der Bestimmung einer topologischen Sortierung vorgestellt, das sowohl aus der Ablaufplanung als auch aus der Software-Entwicklung motiviert werden kann. Schließlich haben wir einen auf Tiefensuche basierenden effizienten Lösungsalgorithmus skizziert und eine dazugehörende Implementierung in C# vorgestellt. Diese ist frei verfügbar und kann gerne ausprobiert werden!
Weitere Artikel:
➡ DAS RUCKSACKPROBLEM
➡ TRAVELING SALESPERSON PROBLEM
➡ DYNAMISCHE PROGRAMMIERUNG
➡ GANTT CHARTS IN DER TOURENPLANUNG